Història del nombre Pi

Va ser el matemàtic gal·lès William Jones (1675-1749) qui va introduir el símbol en 1706 degut al fet a que les paraules perímetre i circumferència comencen per aquesta mateixa lletra.

La història del nombre Pi es pot classificar en dues fases, abans d'Arquímedes i després d'Arquímedes. Això es deu al gran impacte en la manera de pensar dels matemàtics que va comportar aquest. Fins a la seva arribada els mètodes per a fer càlculs eren força pobres, sense estris i pràcticament sense plantejar-se res. El que feien era imaginar la situació i sense fer pràcticament cap mena de càlculs teoritzaven un resultat possible i el donaven per bo.

Part de la primera secció del Papir d'Ahmes o Papir Rhind

El papir conté 87 problemes matemàtics amb qüestions aritmètiques bàsiques, fraccions, càlcul d'àrees, volums, progressions, particions proporcionals, regles de tres, equacions lineals y trigonometria bàsica. També s'hi troba una referència al nombre Pi a causa del següent problema.

Al problema numerat com 50, es diu: "Un camp circular té un diàmetre de 9 khet (1 khet ≈ 50 m). Quina és la seva àrea?"

Actualment ho resoldríem de manera molt simple gràcies a què tenim la següent fórmula i coneixem parcialment el valor de Pi:

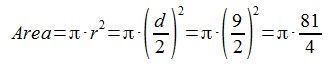
En aquells temps, encara no tenien constància del valor de Pi, però el papir proporciona una fórmula per resoldre el problema que podem aprofitar per deduir el mateix.

64/81*d^2

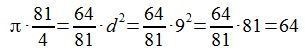
Per tant: Pi*81/4=64

I un cop ho simplifiquem tot, es pot aconseguir una aproximació de Pi:

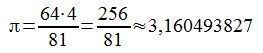
També és curiós que algunes de les piràmides egípcies tenen unes proporcions amb les quals si multipliquem per dos el perímetre de la base i la dividim per l'altura donen aproximacions al nombre Pi. En el cas de la piràmide de Keops s'obté un valor de 3.14297.... Aquests casos són una mica escassos, només unes 3 o 4 de les 90 piràmides que hi ha compleixen aquestes característiques però, hi ha un altre motiu pel qual sabem com de present tenien els egipcis el nombre Pi. Se sap que els enginyers egipcis calculaven les distàncies en colzes reals i els angles en colzes reals partit de dits. Moltes de les piràmides estaven construïdes amb un angle d'1 colze real per a cada 22 dits i la piràmide en què es van aplicar més a la perfecció aquestes dimensions és la Gran Piràmide. Per què és tant important l'ús d'aquesta mesura en l'angle de les piràmides? Doncs la importància d'aquesta mesura és que 1 colze real : 22 dits dona un resultat de 3,14285714 el qual és una aproximació molt bona tenint en compte l'època. L'ús d'aquestes dimensions es devia a què són les més atractives per a l'ull humà i ells ho consideraven la perfecció.

-Mesopotàmia

Una tauleta babilònica anomenada tauleta de Susa afirma que la proporció entre la longitud d'una circumferència i el perímetre d'un hexàgon inscrit és d'1 a 0.96, la qual cosa atorga a pi un valor de 3.125.

Tenim constància de diverses tauletes babilòniques però només es pot arribar a saber gràcies a una.

El que ells utilitzaven com a Pi era 3 i 1/8

-Religió (600 a.C.)

Hi ha referències a la bíblia, al llibre dels reis, que dónen un valor de 3, que ésuna aproximació més dolenta.

<<Hizo el Mar de metal fundido que tenía diez codos de borde a borde; era enteramente redondo, y de cinco codos de altura; un cordón de treinta codos medía su contorno. Debajo del borde había calabazas todo en derredor; daban vuelta al Mar a largo de treinta codos; había dos filas de calabazas fundidas en una sola pieza.>>

I Reyes (Biblia de Jerusalén)

<<Hizo el Mar de metal fundido, de diez codos de borde a borde. Era enteramente redondo y de cinco codos de alto. Un cordón de treinta codos medía su contorno.>>

II Crónicas (Biblia de Jerusalén)

En aquests dos fragments, el valor que donen a Pi, 3, comporta un gran pèrdua de precisió en l'estimació de Pi i no es plantegen ni la possibilitat que sigui més gran de tres.

-Grècia

El matemàtic grec Arquímedes (s. 250 a.C.) va ser el primer en donar una aproximació matemàtica rigorosa a : un valor comprès entre 223/71 i 22/7.

Arquímedes de Siracusa (s. 287 a.C. - s. 212 a.C.) va ser matemàtic, astrònom, filòsof, físic i enginyer. Encara que es coneixen pocs detalls de la seva vida, és considerat un dels científics més importants de l'antiguitat clàssica. L'any 1914, el matemàtic G.H. Hardy va escriure: <<A Arquímedes se'l recordarà quan el dramaturg "Esquilo" hagi sigut oblidat; els idiomes moren, però les idees matemàtiques són permanents. Pot ser que "immortalitat" sigui una paraula un mica absurda, però es possible que els matemàtics tinguin la possibilitat d'aconseguir-la, signifiqui el que signifiqui>> De fet es considera que Arquímedes ha sigut un dels matemàtics i científics més importants que ha habitat el planeta junt amb Isaac Newton, Friedrich Gauss i Leonhard Euler.

Arquímedes va trobar una aproximació del nombre Pi a través d'aproximacions geomètriques donant com a resultat aproximat

3,140845 < Pi < 3,142857

A l'època de Pitàgores, finals del segle 6 a.C. sabien que era 3 i dubtaven del primer decimal.

Claudi Ptolemeu (s.100 d.C.- s.170 d.C.) va ser un astrònom, astròleg, químic, geògraf i matemàtic d'origen grecoegipci que va continuar els plantejaments d'Arquímedes i va arribar a utilitzar polígons de 720 costats per a poder aproximar-se una mica més, va arribar al valor de 3+8/60+30/3600 = 377/120 = 3.14166... amb una precisió de tres decimals.

-Xina

L'astrònom Zhang Heng (78-139) va estudiar el nombre Pi a través de l'aproximació de . Un segle després, l'astrònom Wabg Fang va estimar un valor de 142/45, el qual resulta en 3.1555... tot i que no se sap el mètode que va utilitzar per arribar-hi. Al segle 3 d.C. un matemàtic xinès que es deia Liu Hui amb el mètode d'Arquímedes va arribar fins a 5 decimals correctes utilitzant un polígon de 3072 costats.

A finals del segle V, el matemàtic i astrònom xinès Zu Chongzhi va calcular el valor de 3.1415926, al qual va nomenar com a valor per defecte i 3.1415927 al qual va nomenar com a valor per excés. Va donar dues aproximacions racionals de 22/7 i 355/113, les dues molt conegudes ja que no van poder ser igualades fins al cap de nou segles, al segle XV.

-Índia

De la ÍIndia tenim constància d'uns documents nomenats Siddhantas, que daten del 380 d.C.,i són uns sistemes astronòmics en què el valor de Pi ve estimat com a 3+177/1250, exactament 3,1416, per tant, tres decimals de precisió. Aryabhata, expressa aquest mateix valor en el seu llibre anomenat Aryabhatiya dient <<suma 4 a 100, multiplica per 8 i suma-li 62.000. El resultat dóna aproximadament la circumferència de la qual el diàmetre és 20.000>>

Més tard un matemàtic àrab que es deia Madhava va arribar a l'any 1400 a trobar fins a 11 decimals correctes, en aquest cas utilitzant sèries.

-Egipte modern

Al segle IX d.C. Al-Khwarizmi fa notar en un tractat d'àlgebra que: <<l'home pràctic utilitza 22/7 com a valor de Pi, el geòmetra utilitza 3 i l'astrònom 3.1416>>.

El 1429, Al-Khasi segueix utilitzant el mètode d'Arquímedes i treballa amb polígons fins els 805.306.368 costats per obtenir una aproximació bastant precisa de 14 xifres, que és: 3,14159265358979.

-França

Al segle XVI, el matemàtic Vieta va utilitzar polígons fins a 393.216 costats per obtenir una aproximació precisa però no tant com l'anterior d'Al-Khasi ja que ell va obtenir 9 xifres amb un resultat de 3,141592653.

-Alemanya

El major assoliment amb el mètode d'Arquímedes va ser del matemàtic holandès Ludolf van Ceulen (1540-1610), queva treballar pràcticament al llarg de tota la seva vida en aquesta investigació. Va ser capaç de fer els càlculs amb un polígon de 4.611.686.018.427.387.904 costats aconseguint una aproximació de 35 decimals correctes. Aquesta investigació va ser tan important per a ell que va demanar que a la seva tomba gravessin els 35 nombres que havia tardat tota una vida en trobar. Al seu torn, el seu país va adoptar el nom "nombre de Ludolf" en comptes de Pi per tal de poder commemorar una vida d'esforç.

Època moderna

Durant el segle XVII van començar a utilitzar-se les sèries, els productes infinits i les fraccions contínues. Això ha anat progressant al llarg de la història fins a arribar a l'època dels ordinadors, els quals ens han reemplaçat.

Ranjan Roy deia que el descobriment independent del desenvolupament de la sèrie de Pi <<per persones diferents que vivien en contextos diferents i amb cultures diferents ens dona una idea del caràcter de les matemàtiques com a disciplina universal>>

El mètode de sèrie o successió va ser descobert pel matemàtic alemany Gottfried Wilhelm Leibniz, pel matemàtic i astrònom escocès James Gregory i per un matemàtic indi dels segles XIV o XV del qual la identitat no es coneix amb total certesa (tot i que s'acostuma a atribuir a Nilakantha Somayaji). Leibniz va descobrir aquest mètode el 1673 i Gregory, el 1671.

També hi ha casos en què Pi es troba gràcies al simple atzar i és que el compte de Buffon va demostrar que si es deixa caure una agulla diverses vegades sobre un full pautat i es compta el nombre de vegades que l'agulla toca una de les ratlles, es pot obtenir una bona estimació del valor de Pi. En el cas més simple es pot imaginar que es deixa caure un escuradents sobre un terra de parquet del qual la separació entre les línies és idèntica a la mida de l'escuradents. Per trobar una aproximació de Pi a través d'aquest mètode, n'hi ha prou en tenir en compte el nombre de llançaments fets amb l'escuradents, multiplicar-lo per dos i a continuació dividir-lo pel nombre de cops que l'escuradents toca la línia.

Per acabar, la part històrica del nombre Pi, cal afegir que avui dia els matemàtics opinen que Pi és un nombre <<normal>>, és a dir, que qualsevol patró finit de dígits es dona en la mateixa freqüència en Pi que en una seqüència aleatòria.

De fet, si Pi és un nombre normal, en algun lloc dins les seves interminables xifres existeix, quasi amb total certesa, una representació encertada de cada un de nosaltres: les coordenades atòmiques de tots els nostres àtoms, el nostre codi genètic, els nostres pensaments, etc. Per tant, en certa manera podem pensar que Pi ens fa immortals.

A vegades els matemàtics diuen <<absolutament normal>> per referir-se a una normalitat en qualsevol base i <<normal>> si el nombre ho és en una base en particular. (El nostre sistema decimal, es diu així degut a que la seva base està creada sobre 10 nombres els quals són:0, 1, 2, 3, 4, 5, 6, 7, 8 i 9). La seva normalitat implica que dins de totes les variants possibles de tants dígits possibles, aquests nombres tenen el mateix nombre d'oportunitats d'aparèixer.

El dígit 7, per exemple, hauria d'aparèixer aproximadament un milió de vegades en els deu primers milions de dígits del nombre Pi, i de fet el nombre de cops exacte és de 1.000.207, molt a prop del valor esperat.

El matemàtic i polític francès Émile Borel va donar a conèixer aquest concepte de nombre normal a 1909 com a forma de caracteritzar els dígits de Pi, els quals mostren aparentment una sèrie aleatòria.