Com es troba el nombre Pi?

-Mètode d'Arquímedes (augmentar el nombre de costats dels polígons)

Fer un cercle perfecte en la realitat és impossible ja que sempre tindrà imperfeccions o simplement serà un polígon amb tants costats que simularà un cercle. Tenint això en compte el següent mètode es basa en una lògica simple i fàcil d'entendre.

Sabem que un cercle de diàmetre 1 té com a valor del diàmetre 2πr,per tant l'àrea és 2*1*π que és igual a π.

L'única incògnita que conservem és el nombre Pi i en ser un nombre irracional no hi ha cap mètode per trobar-lo al 100% així que ens hem d'aproximar.

Tal com hem dit abans, si agafem un polígon del qual sí podem calcular el diàmetre de manera exacta i li anem multiplicant el nombre de costats tenim la possibilitat, no d'arribar al cercle perfecte però sí de tenir-ne una aproximació bastant precisa.

Partint d'aquí ens imaginem un quadrat de diagonal 1 i multipliquem els costats per 2 obtenint un octàgon. Això pot ser possible gràcies al teorema de Pitàgores.

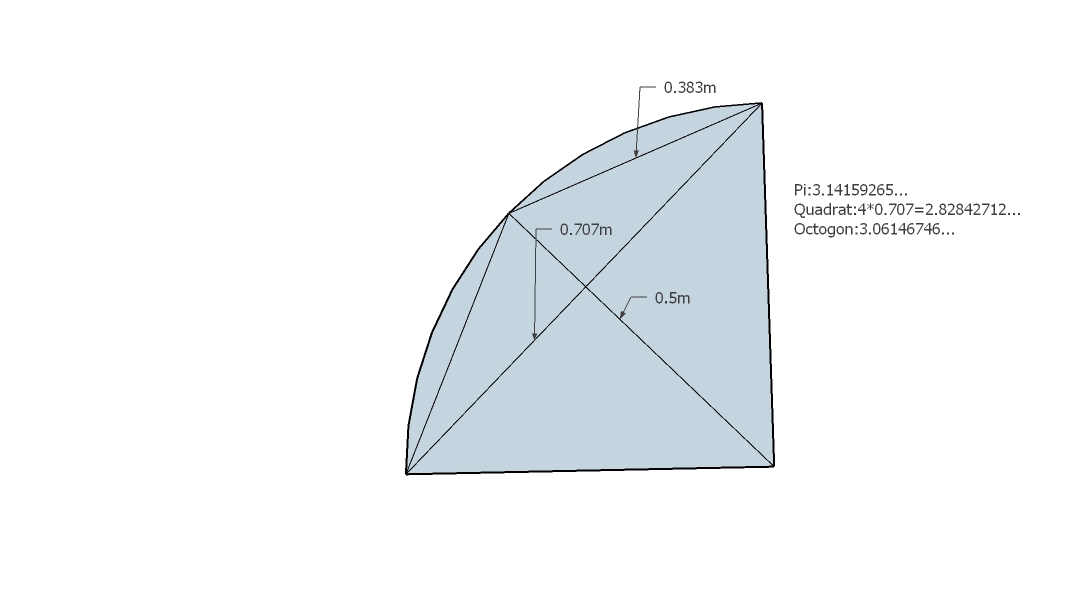
Per tal de poder conèixer la mida dels costats de l'octàgon "z" abans hem de aconseguir la meitat del costat del quadrat "x" i la part de la diagonal de l'octàgon que queda perpendicular al costat del quadrat "w" i "y". Tot això ho farem a través de Pitàgores.

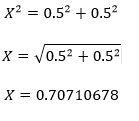
Gràcies a que sabem "x", podrem trobar "w" i amb aquesta tindrem "y

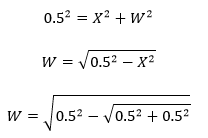
Y és la diagonal de l'octàgon menys "W", per tant:

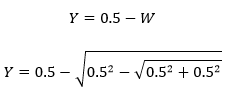
Tenint "Y" i "X" podem aplicar un altre cop Pitàgores i obtenim "Z", que és el costat de l'octàgon

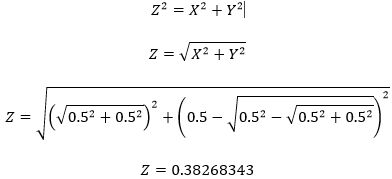
D'aquesta manera, es pot anar augmentant el nombre de costats dels polígons inserits en un cercle a través de Pitàgores.

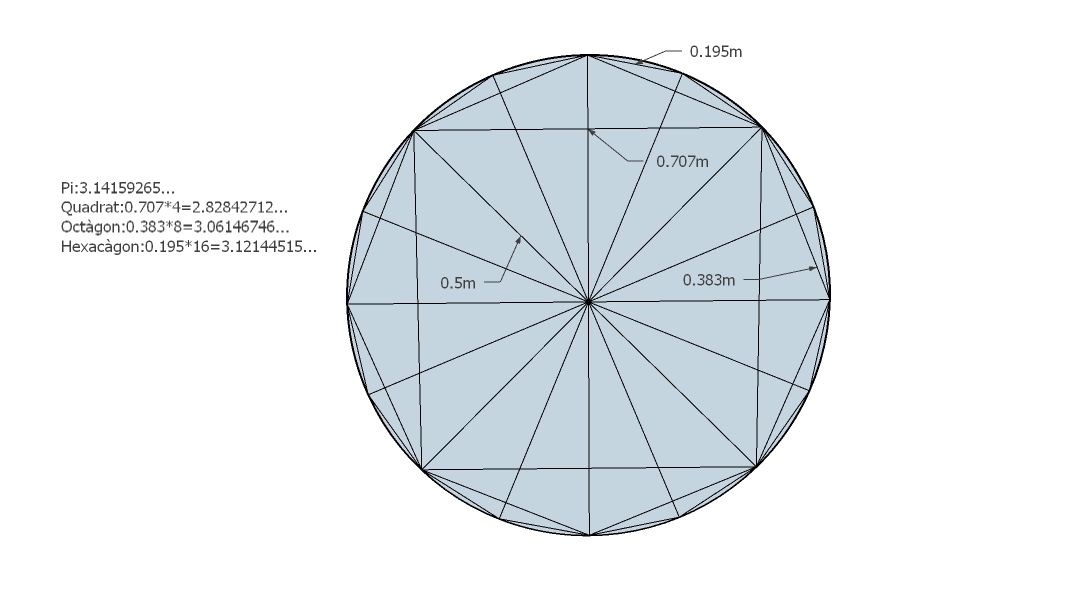
Coneixent aquest sistema per a poder arribar al nombre Pi també es pot desenvolupar una petita equació per tal de poder-hi arribar de manera més directa.

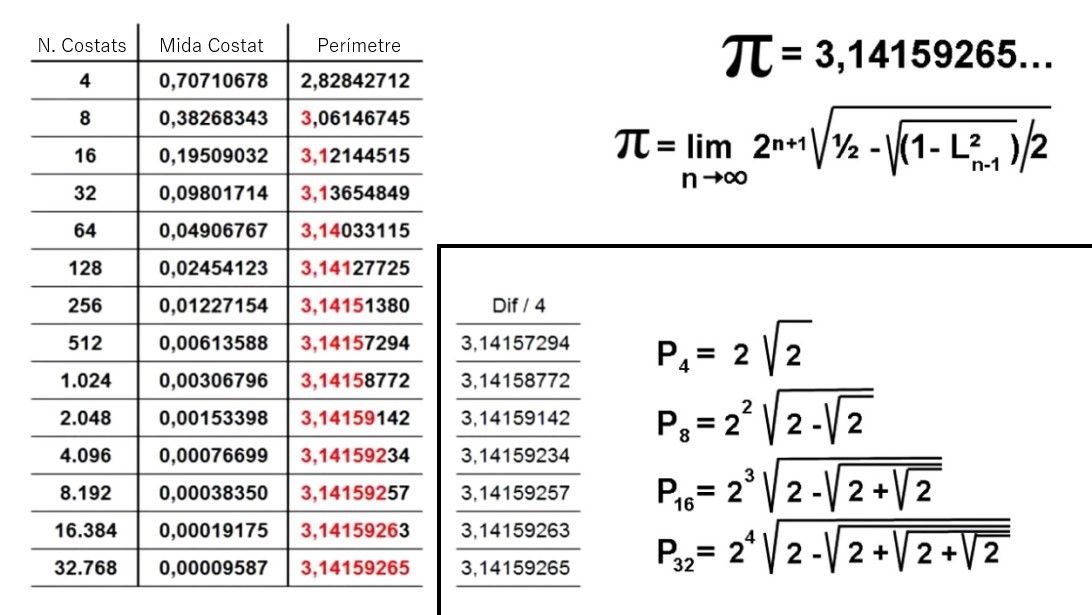
En aquesta fórmula s'expressa un límit en que "n" és el nombre de passos que fem i tendeix a infinit. Un cop anem substituint es pot veure que té la següent simplificació.

-Mètode a partir de successions

Aquest mètode es remunta a l'etapa moderna, en una etapa on els matemàtics disposaven d'ordinadors per tal de fer grans quantitats de càlculs. El principal objectiu d'aquests matemàtics era trobar les sèries més precises, és a dir, que amb menys càlculs l'ordinador pogués trobar més decimals i amb més precisió.

Hi ha moltíssimes sèries fetes per moltíssims matemàtics que van dedicar pràcticament tota la seva vida, de manera que esmentaré les més fàcils d'entendre:

-Nilakantha

Nilakantha: (14 Juny 1444-1544) va ser un matemàtic i astrònom indi posterior a Madhava, el qual va prendre com a referent.

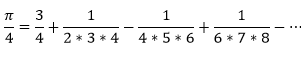
-Leibniz,Gregory i Madhava

Gottfried Wilhelm Leibnitz : (1 juliol 1646 - 14 novembre 1716) va ser un filòsof, científic, matemàtic, lògic, diplomàtic, jurista, bibliotecari i filòleg alemany.

James Gregory: (Novembre 1638 - Octubre 1675) va ser un matemàtic i astrònom escocès.

Madhava de Sangamagrama: (1340-1425) va ser un matemàtic i astrònom indi.

Aquests tres grans matemàtics, van arribar a una fórmula bastant similar entre ells i a excepció de Madhava, Leibniz i Gregory van ser de la mateixa època.

En aquesta successió es diu que una quarta part del nombre Pi equival a 1 més una successió de restes d'1 partit d'un nombre senar més 1 partit del següent nombre senar i així successivament.

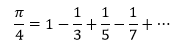
-Euler

Euler: (15 d'abril de 1707- 18 de setembre de 1783) va ser un matemàtic, físic i filòsof suís. Va crear moltes sèries i pràcticament va dedicar tota la seva vida a les matemàtiques però nomes m'he centrat en 5, les dues primeres són bastant similars i les tres següents també ho són entre elles.

1.La primera diu que la meitat de Pi equival a 1 més una successió de l'exponencial dels nombres ordenats partit pels nombres senars multiplicats i ordenats.

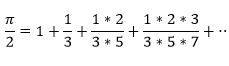
2.La segona diu que la meitat de Pi equival a una successió dels nombres ordenats partits per nombres senars multiplicats per ordre.

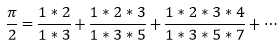
3.La tercera diu que Pi per arrel de 2, tot això partit per 4 equival a 1 més una successió de suma-suma, resta-resta d'1 partit per nombres senars.

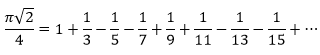
4.La quarta diu que Pi per arrel de tres, tot això partit per 6 equival a una successió d'alternança entre suma i resta d'1 partit pels senars alternats un sí i el següent no.

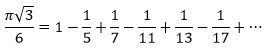
5.La cinquena diu que Pi per arrel de 3, tot això partit per 9 equival a 1 menys una successió d'alternança entre suma i resta d'1 partit per dos nombres parells seguits dels dos senars següents i així consecutivament.

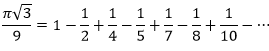
-Mètodes a partir de l'atzar

És força curiós que quan s'apliquen diferents mètodes d'atzar juntament amb aplicacions estadístiques increïblement s'arriben a aconseguir aproximacions al nombre Pi, cosa que demostra que està present en el nostre dia a dia.

-Georges Louis Leclerc

Georges Louis Leclerc, de Bufon (Montbard, Borgonya, 7 de setembre de 1707 - París, 16 d'abril de 1788) va ser un naturalista, matemàtic, botànic, cosmòleg, biòleg i escriptor francès.

Leclerc va ser el descobridor d'un dels principals mètodes d'atzar per a trobar el nombre Pi i el va anomenar les agulles de Bufon.

Aquest mètode consisteix en agafar moltes agulles de les mateixes dimensions i una superfície plana que tingui dibuixada línies paral·leles de les quals la separació sigui la llargada de les agulles. Quan es té això, es deixen caure les agulles de manera aleatòria sobre la superfície amb les línies.

Un cop estan totes les agulles escampades el que s'ha de fer per aconseguir una aproximació de Pi és multiplicar per dos el nombre d'agulles que s'han deixat anar i dividir el resultat entre el nombre d'agulles que tallen les línies, per tant, la probabilitat que una agulla talli una de les línies és 2/π.

He intentat fer una aplicació que simuli l'experiment però no ho he aconseguit. Tot i així, he trobat una aplicació ja feta però aquesta no proporciona una imatge de l'experiment com a tal.

Aquest mètode és capaç de calcular fins a 3 decimals precisos a través de 17 milions de processos/agulles.

-Los Alamos National Laboratory (LANL)

Aquest és un laboratori del departament d'energia dels Estats Units i van ser els descobridors del mètode de Montecarlo.

Aquest mètode es diu així degut al Casino de Montecarlo situat a Mònaco, la capital dels jocs d'atzar. El seu ús com a eina d'investigació prové de la feina realitzada en el desenvolupament de la bomba atòmica durant la Segona Guerra Mundial. El seu ús era la simulació de problemes de probabilitat en la difusió de neutrons en el material de fissió, cosa que té un comportament aleatori.

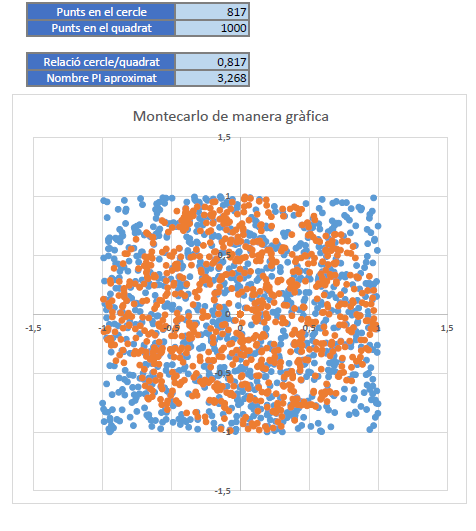
Aquest mètode també és útil a l'hora de calcular Pi de la següent manera:

Si ens imaginem un cercle de radi r inscrit en un quadrat de costat 2r i dividim les àrees de les dues figures, podem aïllar Pi.

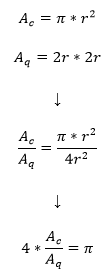
Sabent això, les incògnites que hem de resoldre per a trobar Pi són les àrees del quadrat i del cercle, cosa que podem fer gràcies al mètode de Montecarlo.

Considerant que el centre del quadrat i del cercle estan a 0 en un eix de coordenades, podem fer una simulació en què ens doni punts aleatoris entre y=[-1,1] i x=[-1,1]. Aquesta simulació és força fàcil de fer amb Excel i s'aconsegueix un resultat en què quants més punts aleatoris més precís serà.